Team capacity discharge: how doing things prevents us from doing things
Everybody knows that software needs maintenance. There should be no need to explain what happens to software without maintenance. This is far from controversial in abstract terms but few people are ready discuss the specific numbers. Perhaps even fewer people are willing to accept their implications.
I was once surprised by the perverse simplicity of the problem, which I will describe below.
Say you have a fixed size team ready to start a project. At day one, your team is able to dedicate X hours of work for something to be developed and put to use after your standard unit of development time (month, quarter, year, sprint,...). Once the developed software is in use the team will need Xα hours for maintenance (including support and communication), across the following unit of development time. Naturally, α is a number between 0 and 1, likely in the range of 0.1 to 0.3, which represents the fraction of time that must be assigned to maintenance and can no longer be used for development. The more complexity involved the larger that fraction will be.
Assuming the team has a fixed size, new software development hours over a sequence of consecutive N time units might look like this:
\( X \)
\( X(1 - \alpha) \)
\( X(1 - \alpha)^2 \)
\( X(1 - \alpha)^3 \)
...
\( X(1 - \alpha)^{N-1} \)
In which case, the required maintenance hours might look like this:
0
\( X\alpha \)
\( X\alpha \) + \( X(1 - \alpha) \alpha \)
\( X\alpha \) + \( X(1 - \alpha) \alpha \) + \( X(1 - \alpha)^2 \alpha \)
...
\( \sum\limits_{i = 0}^{N-2} X\alpha(1 - \alpha)^i \)
The last expression represents a simple geometric progression which, unsurprisingly, sums up to:
\( X(1 - (1 - \alpha)^{N-1} ) \)
It had to be that way since the sum of development work and maintenance work efforts must be X.
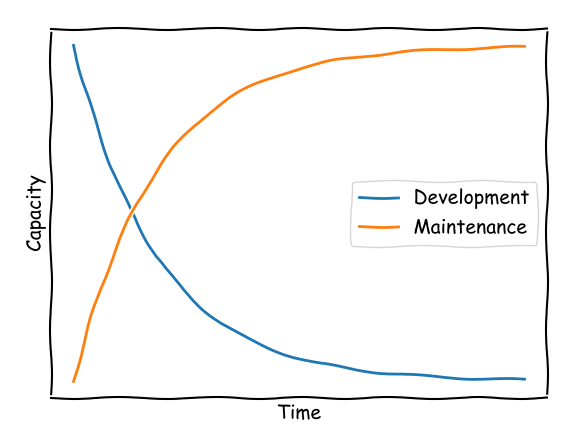
Bottom line: the capacity for development decays exponentially whereas the required capacity for optimal maintenance grows with the symmetric exponential function. Furthermore, the total amount of attainable development time converges to the finite value of X/α, as can be seen by summing the development times of a sequence of consecutive N time units (also a geometric progression) and letting N grow to infinity. At some point nothing can be developed and all the work is related to maintenance.
No... wait. This can't be right. Is this for real? Surely there's something we can do...
Assuming we don't want to neglect maintenance (the results of accumulating technical debt are well known...) here's what you can do:
- exert a conscious effort to control complexity so that α is as low as possible
- gradually discard unused or less frequently used parts of the code
- continuously increase team size
- carefully mix all of the above
So as to ensure constant development capacity without increasing team size we need to discard at the same rate that we assign maintenance. That's where complexity makes a big difference: for smaller values of α the pressure to discard is lower because capacity decays slowly. In fact, it can be easily shown that the time for capacity to be halved is given by
\( t_{1/2} = -{ {ln(2)} \over {ln(1-\alpha)} } \)
A numerical evaluation of the formula above leads to the conclusion that if α=0.3 the capacity for development is halved in approximately 2 units of time, whereas if α=0.1 halving the capacity would take 6.5 units. Decay rates may also be graphically evaluated in the following plot.
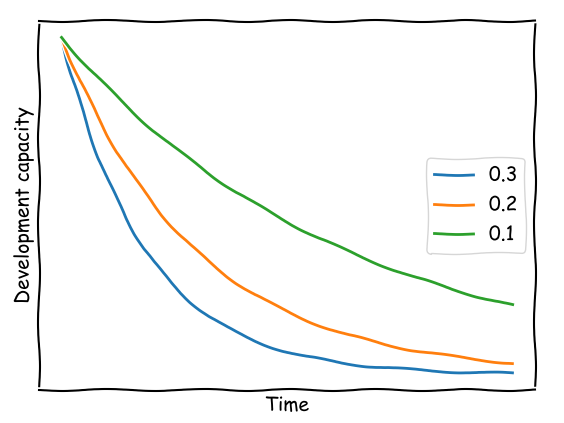
In the real world, the curves are obviously not this smooth - capacity will decay in a series of steps. The need for maintenance can usually be ignored for some time until a third party dependency is discontinued, a third party API changes behaviour, a newly required library can't fit the existing versions... and a big bang of breakage sets in when allegedly nobody expected it to. And then all development has to stop until things are fixed. As the code base increases these incidents happen more and more often until the team can hardly develop anything new. Over the long run, reality will fit the described model with reasonable accuracy.
Perhaps this is something worth considering when taking decisions that might affect implementation complexity.